Stupid Poll Tricks
Or, if you prefer, stupid headline tricks.

I found the following headline amusing because despite the obvious attempt at some Horserace Drama I knew what is almost certainly meant (i.e., not much). Via Fox News, Fox News Poll: Support for Haley doubles in GOP primary, she tops Biden by four.
Here are the dramatic results.
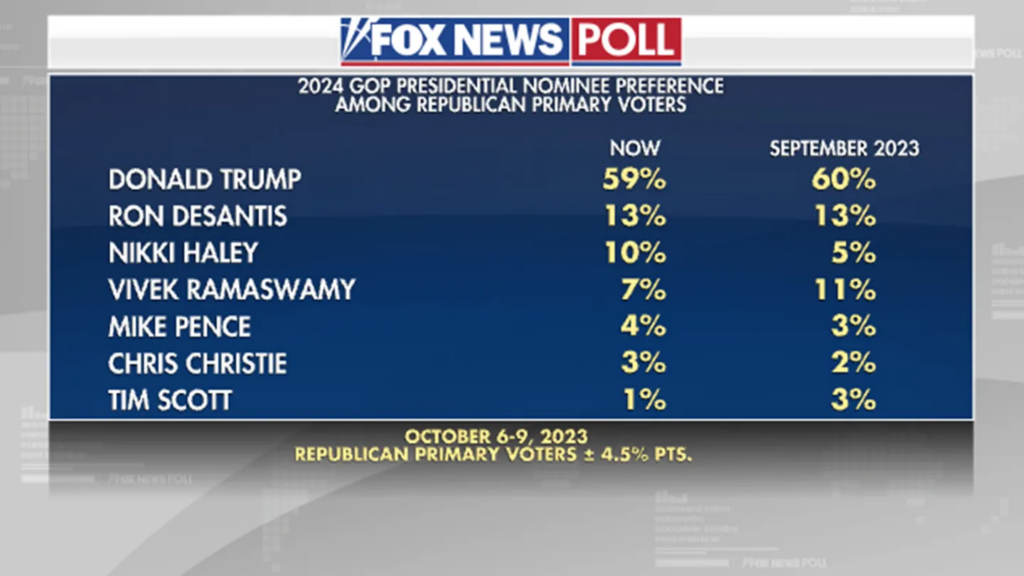
So sure, going from 5% to 10% is a doubling. And she moved into third! We’ll just ignore the that fact that most of the variation is within the MOE and that despite Massive Climb she is still 49 points behind the frontrunner.
Details, details.
And sure, the head-to-head against Biden is nice and all, but we are, shall we say, a ways away from the general.
I am not familiar enough with statistical methods to know exactly how margin of error works, but I do know that it scales.
IOW, the MOE you apply to someone at 59% differs than that for a number like 10%, which in turn is different than what applies to 4%.
4.5% MOE does not mean that someone at 4% might really be at -0.5%.
Sort of OT, but most people don’t understand that MOE is a measure of repeatablity of polling using the exact same methodolgy of sampling etc. In practice, it’s just a different way of saying how large the sample was, not much of a guide to how accurate the poll was as a prediction source.
The Fox poll that shows Trump losing to Biden but Biden losing to either DeSantis or Haley is the one that has potential legs, and I would expect Fox to report on this polling heavily. Report on it enough and they can turn it into a self-fulfilling prophecy of sorts.
@charontwo:
No, because that’s impossible.
But real support could very much be near zero.
Indeed–which means her real support in the broader population could be far closer to 5 than 10.
@Steven L. Taylor:
I would be better placed to argue if I had actually taken a statistics course and could do the real math. Still, I do know enough statistics (part of having a STEM degree) to know 4% at 4.5% MOE might really be 3% or 5%, it is not going to be 1% or 8%.
Again, I do not believe that.
@charontwo:
Ok.
@charontwo: @Steven L. Taylor: I think they usually report the largest MOE for the sample which is the one for whichever is closest to 50%. Thus that MOE is probably for Trump but would be smaller for the rest.
Don’t remember if they are symmetrical around the reoported number.
@J.P. Billingsgate: I would make the modest guess that the more a Republican voter is inclined to support Trump over other Republican candidates, the likelier they are to consider polls that are less favorable to Trump—especially those showing him losing to the senile basement-dweller—to be Deep State propaganda.
@charontwo: @BugManDan: It’s been a long time since my grad school classes on polling methods but this isn’t how political scientists or pollsters interpret sampling error. Yes, it’s simply a function of the sample size (and usually at a confidence level of 95%). But, no, it doesn’t differ proportionately to the candidate’s vote share.
See, for example, “When You Hear the Margin of Error Is Plus or Minus 3 Percent, Think 7 Instead” (NYT) and “5 key things to know about the margin of error in election polls” (Pew Research).
@James Joyner:
I looked at your Pew link, I could not see what you claim is there.
@charontwo:
It’s mostly in Section 1 of the Pew article:
@Neil Hudelson:
That is not the claim I was addressing, I was challenging the idea that 3% MOE means someone with 3% support might really have 6% or 0%. Is that in Pew somewhere, I did not see it.
@charontwo:
That is exactly what that passage says.
@Kurtz:
Not the way I read the passage which talks only about someone at 48%, no mention of how to apply to someone at 3%.
@charontwo:
The article uses 48% as an example to explaining J how MOE works in general. It’s not an article specifically about how MOE impacts someone at exactly 48%.
If they used 27% as an example, with a 3% MOE, then the actual range of support would be 24%-30%. If the candidate was at 3% with a 3% MOE, the spread would be 0% to 6%.
I don’t know why you are insisting it’s applied differently to candidate at different levels of support.
@charontwo: Are you sure you’re not confusing observational error with margin of error?
On the raw figures, Haley has convinced a third of Ramaswamy’s previous supporters that he’s a babbling jackass. I’m surprised it wasn’t more.